Введение

Большинство действий в двигательном репертуаре человека носят отсроченный характер, в то время как немедленные реакции на события окружающего мира составляют хотя и важное, но все же исключение. Отсроченный характер двигательной деятельности требует наличия эффективного способа сохранения в памяти ее внутренней репрезентации. Считается, что внутренняя репрезентация — план будущего движения — формируется на основе «потребного будущего» (Бернштейн, 1966) или, как принято говорить в современной литературе, «ожидаемых сенсорных последствий» (Glover, 2004; Stock, Stock, 2004). Большинство действий представляют собой более или менее сложные упорядоченные последовательности относительно простых двигательных элементов, и это обстоятельство предполагает, что их внутренняя репрезентация должна содержать информацию о порядке выполнения элементов (Bullock, 2004; Rhodes et al., 2004). Следуя традиции, заложенной Н.А. Бернштейном (1966) и A.R Лурия (1969), такие последовательности мы в данной работе будем называть сериями движений, или серийными движениями.

Если речь идет о новой, ранее не встречавшейся серии, то при не слишком больших временных задержках внутренняя ее репрезентация (план серии) сохраняется в рабочей памяти (РП). Традиционная модель РП предполагает, что ее объем ограничен определенным количеством «ячеек» (slots), в каждой из которых может храниться единица информации (Alvarez, Cavanagh, 2004; Baddeley, 2003; Burgess, Hitch, 2005; Luck, Vogel, 1997; и др.). Однако такой подход к пониманию структуры РП подвергается критике (Cowan, 2000) . В последние годы получил развитие альтернативный взгляд, в соответствии с которым РП рассматривается как ограниченный ресурс, распределяемый между всеми одновременно сохраняемыми элементами (Bays et al., 2011; Burnett Heyes, 2012; Fougnie et al., 2012; Gorgoraptis et al., 2011; Zokaei et al., 2011). В таком случае увеличение числа сохраняемых элементов снижает количество информации о каждом элементе, которое может быть сохранено.

Прежде чем серия будет реализована в виде соответствующей последовательности движений, ее внутренняя репрезентация должна быть превращена в моторную форму — в правильно упорядоченную последовательность параметров конкретных движений. Основной вопрос, который обсуждается в настоящей работе, заключается в следующем: в какой момент происходит подобное превращение и, следовательно, в какой форме сохраняется внутренняя репрезентация серии в РП (Abrahamse et al., 2010; Agam et al., 2007; Cisek, 2005; Hudson, Landy, 2012).

При отсроченном воспроизведении серии это превращение может быть выполнено заранее, т.е. в процессе восприятия или за время последующего хранения информации в РП. Но оно может происходить также и непосредственно перед двигательной реализацией серии (pre-programming) или даже в процессе выполнения ее элементов (ongoing programming).

Результаты нашего предыдущего исследования (Корнеев, Курганский, 2013) свидетельствуют о том, что внутренняя репрезентация серии графических движений (ломаных траекторий), сформированная на основе статической информации (симультанной карты движений) или динамической информации (наблюдение за движением объекта по маршруту), сохраняется не в моторной, а, скорее всего, в перцептивной форме (в виде пространственных кодов). В пользу такой точки зрения говорит обнаруженная в этой работе выраженная зависимость времени реакции и времени движения от длительности удержания следа в РП. Время реакции (или латентный период двигательной реакции) — это интервал времени между началом выполнения движений и началом предъявления стимула. Время реакции содержит информацию о длительности происходящих в РП процессов, в частности процессов формирования и преобразования внутренней репрезентации серийного движения. Полученные ранее результаты указывают на поздний характер преобразования внутренней репрезентации последовательности из немоторной формы в моторную. Однако результаты работы (Корнеев, Курганский, 2013) не позволяют ответить на вопрос: информация о предстоящем движении преобразуется в моторную форму в течение латентного периода или также и во время выполнения последовательности графических движений? В частности, остается неизвестным, когда именно происходит преобразование информации о порядке выполнения элементов.

При необходимости запомнить и воспроизвести новое серийное движение, заданное с помощью движущегося в зрительном поле объекта (такая ситуация возникает, например, при имитации одним человеком движений другого человека), порядок выполнения движений-элементов становится известен уже на стадии зрительного предъявления. Если внести дополнительное условие — воспроизводить последовательность движений в порядке, обратном исходному порядку предъявления ее элементов, — то потребуется дополнительная когнитивная операция преобразования порядка. Если эта операция происходит на ранних этапах (в пространстве исходных перцептивных кодов), то временные издержки, связанные с ее выполнением, не скажутся ни на длительности латентного периода, ни на временной структуре серии движений. В процессе обращения порядка элементов последовательности в РП должны параллельно сосуществовать две версии последовательности — исходная и формируемая обратная. Поэтому в соответствии с традиционными моделями РП можно ожидать возрастания числа ошибок (пропусков, замен элементов и проч.), а в соответствии с ресурсной моделью РП — снижения точности, с которой сохраняются сведения о длинах и пространственной ориентации сегментов ломаной траектории.

Напротив, при позднем преобразовании операция обращения порядка элементов может увеличить латентное время копирования (при построении моторной программы непосредственно перед движением) или сказаться на темпе выполнения движений последовательности (при планировании в процессе движения). В этом случае обращение порядка элементов в процессе выполнения последовательности не требует наличия двух версий последовательности (поскольку обращенная последовательность формируется вовне и доступна перцептивно). Соответственно нет оснований ожидать увеличения числа ошибок и/или снижения пространственной точности воспроизведения элементов серии.

Дополнительную возможность проверить, происходит ли изменение порядка выполнения последовательности на этапе ее восприятия или же позже, во время ее двигательной реализации, предоставляет исследование эффектов недавности (recency effect) и первичности (primacy effect). Эффект недавности заключается в том, что последние элементы серии запоминаются лучше, чем элементы в ее середине, а эффект первичности — в том, что первый элемент воспроизводится точнее, чем последующие (Аткинсон, Шиффрин, 1998; Gorgoraptis et al., 2011; Murdock, 1962). При этом эффект первичности обычно выражен сильнее эффекта недавности (Rhodes et al, 2004). Данные исследований, посвященных особенностям прямого и обратного серийного воспроизведения, свидетельствуют о том, что при обращении порядка происходит усиление эффекта «недавности» и ослабление эффекта «первичности» (см. обзор: Hurlstone et al., 2004). В свете имеющихся данных представляется интересным проанализировать наличие и силу этих эффектов на материале серийных движений. Поскольку при обращении порядка элементов последовательности первый и последний элементы меняются местами, при раннем обращении порядка следует ожидать, что эффекты первичности и недавности тоже поменяются местами. Напротив, в случае обращения порядка на поздних этапах нет основания ожидать, что такая замена произойдет.

Для того чтобы проверить, какие из этих возможностей реализуются в действительности, был проведен эксперимент, в котором сравнивались длительность латентной фазы и временная структура последовательности графических движений, заданных движущимся объектом и воспроизводимых испытуемыми в прямом и обратном порядке.

Методика эксперимента

В эксперименте участвовали 14 взрослых испытуемых (6 мужчин, 8 женщин, средний возраст — 25 лет). Испытуемые были проинформированы о характере предстоящей экспериментальной процедуры и выразили согласие на участие в исследовании. Все испытуемые были практически здоровы, характеризовались предпочтением правой руки (по самоотчету), а также нормальным (или корригированным) зрением.

Задача испытуемого состояла в том, чтобы, наблюдая за движущимся по невидимой траектории курсором, запомнить эту траекторию и в ответ на подачу императивного сигнала воспроизвести (скопировать) ее на графическом планшете.

В качестве стимулов использовался набор из 32 различных траекторий — незамкнутых ломаных, состоящих из 6 вертикальных или горизонтальных сегментов (рис. 1). Курсором служил квадрат со стороной 3 мм.

Для предъявления стимулов использовался дисплей с диагональю 40 см и частотой кадровой развертки 60 Гц. Движения записывались с помощью графического планшета (Wacom Intuos3, формат А5) с частотой оцифровки 100 Гц и пространственным разрешением 200 линий на мм.

Каждая проба начиналась с появления фиксационной точки в течение 1000 мс, после чего в течение 3000 мс предъявлялся движущийся вдоль траектории курсор. По окончании стимуляции с задержкой, варьируемой в пределах от 0 до 3000 мс, подавался короткий тональный звуковой императивный сигнал. В ответ на этот сигнал испытуемый должен был как можно быстрее начать воспроизведение запомненной траектории и выполнять ее максимально быстро, стараясь избегать ошибок, но не исправляя уже допущенные ошибки.

Рис. 1. Примеры траекторий, предъявляемых в эксперименте

Для исключения потенциального влияния лево-правой и верхненижней асимметрии на двигательный ответ испытуемого направление первого движения влево, вправо, вверх, вниз в блоке проб встречалось одинаково часто. Начальная точка движения при этом была одна и та же — движение начиналось из центра планшета, это задавалось инструкцией.

Эксперимент был построен по 2x4 внутрииндивидуальной схеме, в которой факторами служили порядок воспроизведения («прямой» или «обратный», далее ПОРЯДОК) и время удержания следа в рабочей памяти (0, 500, 1000 и 3000 мс, далее ЗАДЕРЖКА). Сессия эксперимента состояла из двух блоков проб. В одном блоке испытуемый воспроизводил траекторию в прямом порядке, в другом — в обратном порядке. Порядок выполнения блоков в пределах сессии был уравновешен: половина испытуемых сначала выполняла пробы в прямом порядке, а затем в обратном; вторая половина испытуемых придерживалась противоположного порядка выполнения блоков. Эти два блока проб формировались за счет двукратного предъявления каждой из 32 траекторий, порядок траекторий определялся квазислучайно, отдельно для каждого испытуемого. При этом 4 уровня фактора ЗАДЕРЖКА были с равной вероятностью псевдослучайным образом распределены среди 64 проб блока, каждый уровень этого фактора (0, 500, 1000 и 3000 мс) встречался за время выполнения блока проб ровно 16 раз.

Обработка результатов

Записанные траектории движений — зависимости координат кончика электромагнитного пера планшета от времени — использовались для определения латентного времени (reaction time, RT) воспроизведения траектории, средней длительности движения (moving time, МТ) вдоль одного сегмента траектории и длительности промежуточных остановок в углах траектории (dwelling time, DT).

Процедуры определения этих величин подробно описаны в нашей предыдущей работе (Корнеев, Курганский, 2013). Путём визуального сопоставления воспроизведенной траектории с образцом для каждого испытуемого определялось число ошибок. К ошибкам воспроизведения траектории относили неправильное число сегментов (усложнение или упрощение), значительное, затрудняющее узнавание фигуры, искажение при правильном числе сегментов, а также достаточно редко встречающиеся пространственные искажения, в результате которых вся траектория или отдельные ее элементы отражаются относительно горизонтальной или вертикальной оси.

В соответствии с описанными выше представлениями о РП как о ресурсе с ограниченной разрешающей способностью при увеличении количества элементов запоминаемой последовательности можно ожидать снижения качества репрезентации последовательности и увеличения разброса величины углов между элементами при воспроизведении траектории. С этой целью были посчитаны углы между элементами в записях ответов испытуемых. При этом в анализ включались как правильно, так и ошибочно воспроизведенные траектории с числом элементов от 5 до 8. В каждой из анализируемых траекторий измерялись все углы между элементами и затем рассчитывалось стандартное отклонение полученного набора значений. Эти стандартные отклонения усреднялись отдельно для каждой из встречающихся длин траекторий (от 5 до 8). Поскольку при воспроизведении ломаных испытуемые могли пропустить элементы или добавить лишние, количество воспроизведенных элементов можно рассматривать как апостериорный фактор.

С целью оценки пространственной точности выполнения отдельных элементов серии (сегментов траектории) в зависимости от места в серии был проведен анализ стабильности их ориентации относительно горизонтальной и вертикальной осей. Для этого отдельно у каждого элемента каждой траектории вычислялся угол, под которым он находится к горизонтальной оси планшета. Если этот угол оказывался больше 45 градусов, то элемент считался вертикальным и рассчитывался угол его отклонения от вертикальной оси планшета. Далее вычислялось стандартное отклонение полученных угловых значений для элементов в зависимости от порядка их предъявления. В данном случае в анализ были включены только траектории, состоящие из 6 элементов, поэтому в результате было получено по 6 стандартных отклонений — для первого, второго и т.д. элементов.

Результаты эксперимента и их обсуждение

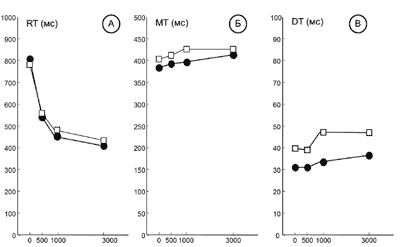
Величины латентного периода (RT), времени движения вдоль одного сегмента (МТ) и длительности промежуточных остановок в углах траектории (DT) были подвергнуты дисперсионному анализу (rmANOVA) с внутри-индивидуальными факторами ПОРЯДОК (прямой или обратный) и ЗАДЕРЖКА (0, 500, 1000 и 3000 мс).

Оказалось, что фактор ПОРЯДОК влияет на величину DT (F(l, 13)=5.13, р=0.041), но не влияет ни на RT (F(l, 13)=0.749, р=0.402), ни на МТ (F(l, 13)=1.564, р=0.233). Фактор ЗАДЕРЖКА, напротив, оказывает высоко значимое влияние на RT (F(3,11)=34.402, р<0.0005) и МТ (F(3, 11)=21.733, р<0.0005), но никак не влияет на DT (F(3, 11)= 1.441, р<0.284). Ни для одной из трех величин не было обнаружено значимого взаимодействия факторов ПОРЯДОКхЗАДЕРЖКА (все р>0.326).

Полученные эффекты иллюстрирует рис. 2, из которого видно, что время реакции RT монотонно убывает с ростом длительности удержания следа в РП. Характер этой зависимости (затухающая экспонента) качественно соответствует полученным ранее результатам (Корнеев, Курганский, 2013) и подтверждает тот факт, что внутренняя репрезентация последовательности движений не является статической, а представляет собой процесс преобразования полученной сенсорной информации в перцептивные коды. Причем этот процесс активно протекает по крайней мере в течение 3 секунд. Отсутствие различий во времени реакции при прямом и обратном воспроизведении может свидетельствовать как в пользу того, что процесс обращения порядка происходит на ранних этапах — в процессе восприятия стимула или сразу после окончания его предъявления, так и в пользу того, что он осуществляется в процессе выполнения последовательности. В пользу второй возможности также свидетельствует значимо большее время промежуточных остановок при обратном воспроизведении — явление, которое обычно связывают с уточнениями и текущим построением программы в процессе движения (ongoing programming).

На рис. 3 показано среднее число ошибок при прямом и обратном воспроизведении для разных значений времени задержки. Хотя приведенные на этом рисунке графики показывают тенденцию к увеличению числа ошибок с ростом времени удержания следа в РП, а также несколько большее число ошибок при воспроизведении траектории в прямом порядке, эти эффекты оказались статистически незначимы. Дисперсионный анализ (rmANOVA) с внутрииндивидуальными факторами ПОРЯДОК (прямой или обратный) и ЗАДЕРЖКА (О, 500, 1000 и 3000 мс) показал, что влияние каждого из факторов и их взаимодействия не достигает уровня значимости (р>0.2 во всех случаях).

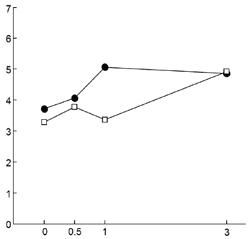
Рис. 3. Зависимость усредненного по группе испытуемых количества ошибок (ось ординат) от величины задержки Д (ось абсцисс) для прямого (круги) и обратного (квадраты) порядка воспроизведения. Величина задержки Д дана в секундах

Отсутствие влияния обращения порядка воспроизведения на количество допускаемых ошибок свидетельствует о формировании последовательности в процессе воспроизведения траектории. В этом случае при обращении порядка нет необходимости удерживать в РП одновременно две последовательности — прямую и обратную, что делало бы задачу более сложной и приводило бы к заметному увеличению числа ошибок при воспроизведении в обратном порядке.

Зависимость меры стабильности воспроизведения углов между элементами от длины воспроизводимой траектории при прямом и обратном ее воспроизведении показаны на рис. 4. Дисперсионный анализ (rmANOVA) с внутрииндивидуальными факторами КОЛИЧЕСТВО ЭЛЕМЕНТОВ (5, 6, 7 и 8) и ПОРЯДОК (прямой или обратный) показал, что оба фактора не влияют на стабильность угла между элементами (р<0.2 в обоих случаях). Взаимодействие факторов также не оказало значимого влияния на оцениваемый параметр (р=0.416).

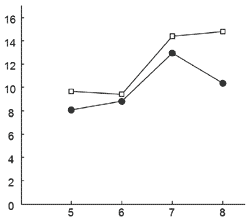
Рис. 4. Зависимость стабильности углов между элементами последовательности от длины траектории для прямого (круги) и обратного (квадраты) порядка воспроизведения. По оси абсцисс указано количество элементов в последовательности, по оси ординат — стандартное отклонение углов между элементами

Описанные выше результаты можно рассмотреть в контексте «ресурсной» модели РП, согласно которой при увеличении числа элементов снижается точность и полнота информации о каждом из них. В таком случае полученные данные свидетельствуют в пользу того, что обращение порядка не связано с увеличением количества удерживаемых в РП элементов. Пространственные характеристики воспроизводимых испытуемыми траекторий не меняются при обращении порядка. Этот факт, как и предыдущие результаты, свидетельствует в пользу гипотезы позднего формирования порядка элементов и обращения их порядка.

Надо отметить, что количество элементов тоже не влияет на стабильность размера углов между элементами траектории, что противоречит предсказаниям «ресурсной» модели РП. Не исключено, что причина этого заключается в недостаточно большой выборке траекторий с 5 и 8 элементами (их обнаружилось всего 5% от общего числа).

Средние значения меры разброса ориентации сегмента в зависимости от порядкового номера его предъявления при прямом и обратном воспроизведении показаны на рис. 5.

Дисперсионный анализ (rmANOVA) с внутрииндивидуальными факторами НОМЕР ЭЛЕМЕНТА (от 1 до 6) и ПОРЯДОК (прямой или обратный) показал, что ни один из этих факторов не оказывает значимого влияния на стабильность выполнения элементов (р>0.8 для обоих факторов). При этом взаимодействие факторов в данном случае оказалось значимым (F(5,9)=6.877, р=0.007).

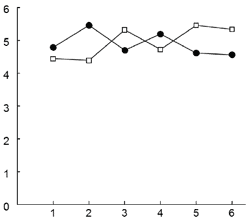
Рис. 5. Зависимость стабильности ориентации элементов от их порядкового номера для прямого (круги) и обратного (квадраты) порядка воспроизведения. По оси абсцисс указан номер элемента, по оси ординат — стандартное отклонение угла наклона элемента

Характер влияния взаимодействия факторов можно оценить по рис. 5. При прямом воспроизведении (черные кружки) усредненные стандартные отклонения первых элементов относительно высоки, а к последним элементам этот показатель падает (т.е. качество двигательной реализации повышается).

В данном случае можно говорить о наличии эффекта недавности (recency effect) и отсутствии эффекта первичности (primacy effect). При обратном воспроизведении, напротив, от 1 к 6 элементу качество ухудшается, т.е., напротив, наблюдается эффект первичности и отсутствует эффект недавности. Хотя такая картина не соответствует ни имеющимся данным, полученным другими исследователями (см. Hurlstone et al., 2014), ни сформулированным выше гипотезам, тем не менее эти данные можно проинтерпретировать следующим образом. Эффект изменения качества связан не столько с порядком предъявления элементов, сколько с порядком их воспроизведения. Если предположить, что формирование порядка элементов происходит в процессе выполнения движений, то полученную картину можно объяснить тем, что в начале выполнения точность воспроизведения пространственных параметров снижена за счет загруженности процессами построения программы из многих элементов. Между тем выполнение последних элементов происходит в ситуации, когда серийный порядок уже сформирован и первые элементы последовательности реализованы. В этом случае естественно ожидать более высокой точности воспроизведения пространственных параметров элементов.

Таким образом, выбранный параметр — стабильность ориентации элемента в зависимости от его положения в серии — оказался чувствителен к порядку воспроизведения элементов. Полученные данные указывают на то, что этот параметр изменяется в процессе выполнения серийного действия, что в свою очередь позволяет говорить о том, что процесс построения последовательности происходит на позднем этапе.

Заключение

Полученные в настоящем исследовании результаты свидетельствуют о том, что замена исходного, заданного во время зрительного предъявления, порядка следования сегментов на противоположный не оказывает влияния на длительность латентной фазы воспроизведения последовательности, а также не сказывается на числе ошибок при выполнении и на вариативности пространственных параметров элементов траектории. Тем не менее обращение исходного порядка элементов приводит к хотя и незначительному по абсолютной величине, но статистически значимому влиянию на длительность пауз, возникающих в вершинах траектории.

Отсутствие выраженного влияния порядка выполнения последовательности на число ошибок и меры вариативности ее элементов, а также полученное сочетание двух обнаруженных фактов — нечувствительности длительности латентного периода и чувствительности фазы реализации движения к обращению порядка выполнения элементов серии — делает маловероятным предположение о том, что процесс обращения траектории происходит во время наблюдения или в течение латентного периода. Скорее, полученные данные соответствуют представлениям о текущем программировании (Alouche et al., 2012), т.е. идее о превращении внутренней репрезентации сложного движения из абстрактной или перцептивной формы в моторные коды параллельно с ее двигательной реализацией.

Таким образом, результаты исследования указывают на то, что последовательность сегментов траектории запоминается в исходном порядке и замена порядка ее элементов на обратный происходит, по-видимому, непосредственно в процессе реализации серии движений.

Список литературы

1. Аткинсон Р, Шиффрин Р. Управление кратковременной памятью // Психология памяти / Под ред. Ю.Б. Гиппенрейтер, В.Я. Романова. М.: ЧеРо, 1998. С. 508—547.
2. Бернштейн Н.А. Очерки по физиологии движений и физиологии активности. Москва: Медицина, 1966.
3. Корнеев А.А., Курганский А.В. Внутренняя репрезентация серии движений при воспроизведении статического рисунка и траектории движущегося объекта // Журн. высш. нерв, деятельности им. И.П. Павлова. 2013. Т. 63. № 4. С. 437—450.
4. Лурия А.Р. Высшие корковые функции человека и их нарушения при локальных поражениях мозга. 2-е изд. М.: Изд-во Моек, ун-та, 1969.
5. Abrahamse E.L., JimenezL., Verwey W.B., Clegg В. A. Representing serial action and perception // Psychonomic Bulletin and Review. 2010. Vol. 17. N 5. P. 603—623.
6. Agam Y, Galperin H., Gold B.J., Sekuler R. Learning to imitate novel motion sequences // Journal of Vision. 2007. Vol. 7. N 5 (1). P. 1—17.
7. Alouche S.R., SantAnna G. N., Biagioni G., Ribeiro-do-Valle L.E. Influence of cueing on the preparation and execution of untrained and trained complex motor responses // Brazilian Journal of Medical and Biological Research. 2012. Vol. 45. N 5. P. 425—435.
8. Alvarez G. A., Cavanagh P. The capacity of visual short-term memory is set both by visual information load and by number of objects // Psychological Science. 2004. Vol. 15. N 2. P. 106—111.
9. Baddeley A. Working memory: Looking back and looking forward // Nature Reviews Neuroscience. 2003. Vol. 4. N 10. P. 829—839.
10. BaysP.M., GorgoraptisN., WeeN. et al. Temporal dynamics of encoding, storage, and reallocation of visual working memory // Journal of Vision. 2011. Vol. 11. N 10 (6). P. 1—15.
11. Bullock D. Adaptive neural models of queuing and timing in fluent action // Trends in Cognitive Sciences. 2004. Vol. 8. N 9. P. 426—433.
12. Burgess N., Hitch G. Computational models of working memory: putting long-term memory into context // Trends in Cognitive Sciences. 2005. Vol. 9. N 11. P. 535—541.
13. Burnett Heyes S., Zokaei N., van der Staaij I. et al. Development of visual working memory precision in childhood // Developmental Science. 2012. Vol. 15. N 4. P. 528—539.
14. Cowan N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity // Behavioral and Brain Sciences. 2000. Vol. 24. N 1. P.87—114.
15. CisekP. Neural representations of motor plans, desired trajectories, and controlled objects // Cognitive Processing. 2005. Vol. 6. N 1. P. 15—24.
16. Fougnie D., Suchow J. W., Alvarez G.A. Variability in the quality ofvisual working memory // Nature Communications. 2012. Vol. 3. P. 1229.
17. Glover S. Separate visual representations in the planning and control of action // Behavioral and Brain Sciences. 2004. Vol. 27. N 1. P. 3—24.
18. GorgoraptisN., Catalao R.F., BaysP.M., Husain M. Dynamic updating of working memory resources for visual objects // The Journal of Neuroscience. 2011. Vol. 31. N23. P.8502—8511.
19. Hudson T.E., Landy M.S. Motor learning reveals the existence of multiple codes for movement planning // Journal of Neurophysiology. 2012. Vol. 108. N 10. P. 2708—2716.
20. Hurlstone M.J., Hitch G.J., Baddeley A.D. Memory for serial order across domains: An overview of the literature and directions for future research // Psychological Bulletin. 2014. Vol. 140. N 2. P. 339—373.
21. Luck S.J., Vogel E.K. The capacity of visual working memory for features and conjunctions // Nature. 1997. Vol. 390. N 6657. P. 279—281.
22. Murdock Jr B.B. The serial position effect of free recall // Journal of Experimental Psychology. 1962. Vol. 64. N 5. P. 482.
23. Rhodes B.J., Bullock, D., Verwey, W.B. et al. Learning and production of movement sequences: Behavioral, neurophysiological, and modeling perspectives // Human Movement Science. 2004. Vol. 23. N 5. P. 699—746.
24. Stock A., Stock C. A short history of ideomotor action // Psychological Research. 2004. Vol. 68. N 2—3. P. 176—188.
25. Zokaei N., Gorgoraptis N., Bahrami B. et al. Precision of working memory for visual motion sequences and transparent motion surfaces // Journal of Vision. 2011. Vol. 11. N 14. P. 1—18.